DES is a block cipher which is based on a Fiestel Cipher structure where encryption is carried out in multiple rounds, each of which uses a different subkey derived from the original key. The encryption/decryption is done on blocks of 64 bit with a 56 bit long key. The encryption/decryption completes in 16 rounds, where each round uses a 48 bit subkey.
Each round follows the following steps:
- Partition of the input block into two equal halves
- DES function of the right half and the subkey
- XOR of the left half with the output of the function
Now let me explain each steps in detail,
DES Encryption:
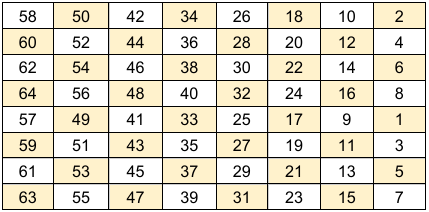
- The bits of the plain text is permuted by the initial permutation table which is shown in the following figure.
Eg. Plain Text, M = 0123456789ABCDEF
M (in binary) = 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
M (after permutation) = 1100 1100 0000 0000 1100 1100 1111 1111 1111 0000 1010 1010 1111 0000 1010 1010
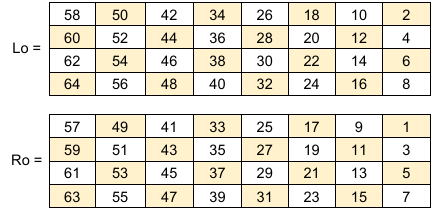
2. The permuted bits is then divided into two equal halves L0 and R0
L0 = 1100 1100 0000 0000 1100 1100 1111 1111
R0 = 1111 0000 1010 1010 1111 0000 1010 1010
3. Li = Ri-1
Ri = Li-1 ⊕ f(Ri-1, Ki)
Finding f(Ri-1, Ki)
Let the key given be K = 133457799BBCDFF1
K (in binary) = 0001 0011 0011 0100 0101 0111 0111 1001 1001 1011 1011 1100 1101 1111 1111 0001
The 64 bit key is permuted by the key permutation table which is given below, to obtain a 56 bit key after discarding the parity bits.
K (after permutation) = 1111 0000 1100 1100 1010 1010 1111 0101 0101 0110 0110 0111 1000 1111
Now divide K into two equal parts, Co and Do containing 28 bits each
Co = 1111 0000 1100 1100 1010 1010 1111
Do = 0101 0101 0110 0110 0111 1000 1111
From this we have to obtain Ci and Di for 16 rounds from which the subkeys are created. The Ci and Di for the first round is obtained by left shifting Co and Do by 1,
C1 = 1110 0001 1001 1001 0101 0101 1111
D1 = 1010 1010 1100 1100 1111 0001 1110
By permuting C1 and D1 by the following table the subkey K1 is obtained which is of 48 bit long.
K1 = 0001 1011 0000 0010 1110 1111 1111 1100 0111 0000 0111 0010
Likewise C2 and D2 is obtained from C1 and D1 by doing left shift by 1 and K2 is obtained by passing C2 and D2 to PC-2. Similarly Ci and Di is obtained from Ci-1 and Di-1 by doing left shift according to the following table,
____________________________________________________________________________________ | Round | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ |Left-Shifts| 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Now, the R0 has to be passed to an extension table which makes it 48 bits from 32 bits,
Thus, E(R0) = 0111 1010 0001 0101 0101 0101 0111 1010 0001 0101 0101 0111
E(R0) ⊕ K1 = 0110 0001 0001 0111 1011 1010 1000 0110 0110 0101 0010 0101
The result of E(R0) ⊕ K1 is written in form of 8 rows with 6 bits each as follows,
B1 = 011000 B2 = 010001 B3 = 011110 B4 = 111010
B5 = 100001 B6 = 100110 B7 = 010100 B8 = 100101
There are 8 S-boxes which gives a 4 bit output when a 6 bit input is given, each Bi is given as input to S-boxes of corresponding i value.
How to lookup in a S-Box?
It’s simple, the first and last bit determines the row and the other four determines the column and the value inside that box is the required 4 bit output.
The result from the S boxes => 0101 1100 1000 0010 1011 0101 1001 1110 is then permuted by the following permutation table,
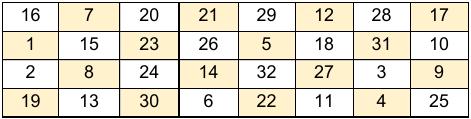 After doing the permutation what we finally get is the value of f(R0, K1). It is then XOR with L0 to get R1. Similarly the process is repeated 16 times. After the 16th round L16 and R16 is reversed ie,
After doing the permutation what we finally get is the value of f(R0, K1). It is then XOR with L0 to get R1. Similarly the process is repeated 16 times. After the 16th round L16 and R16 is reversed ie,
L16 = 0100 0011 0100 0010 0011 0010 0011 0100
R16 = 0000 1010 0100 1100 1101 1001 1001 0101
becomes, R16L16 => 0000 1010 0100 1100 1101 1001 1001 0101 0100 0011 0100 0010 0011 0010 0011 0100 which is permuted with the final permutation table IP-1 to get the cipher text.
DES Decryption:
Decryption is also done in the same manner in the reverse order.